Intro to Numerical Computation with Molecular Dynamics
All the problems that we solved until our undergraduation involved balls falling freely in gravity, boxes sliding down an inclined plane or two monkeys hanging on a pulley. We know that all such problems have a solution, only if we were as creative to come up with a way out. What about a slightly complicated problem? For example, we want to understand the flow of fluid through a complex set of pipes or the evolution of a gas in a nano cavity. We can quickly understand that we can no longer solve them by hand. It is not only difficult but also cumbersome. In some cases, there is no analytical solution available for even a marginally complex system like the quantum mechanical solutions of an electron in a molecule. Numerical solution gives us a way to get over these obstacles and observe the properties of real world systems.
How useful is this system really, you might think. But, almost all of the modern day development relies on our capacity to solve the numerical problems. Starting from the band structure of Si based on which your computer is made to the trajectories of the satellites which are launched. These very numerical solutions become very critical in chemistry and material sciences where the properties of a giant molecule or a new material needs to be predicted. Also, in biological sciences where the function of some complex molecules and enzymes in our body needs to be known. In the present day, understanding physics without the touch of numerical computation is not possible atleast in the life of a graduate student, in my opinion. Another reason is that it makes it very exciting to learn theories which can be applied on some real physical systems in nature. This post is an attempt to introduce you to computational physics using a simple example in molecular dynamics.
The Basics: How complicated is scientific computation?
The crux of all the problems in physics is to understand that we end up with a differential equation which needs to be solved to determine the required parameters. Take the system of a ball falling freely from a certain height. It ends up with the following equations.
$$ v_y = gt$$ $$ y = \frac{1}{2} gt^2 $$
Where $t$, $y$ and $v_y$ are time, height and vertical velocity respectively. They can also be written in the differential form as shown below.
$$\frac{dy}{dt} = gt$$ $$\frac{d^2y}{dt^2} = g $$
We can see that the problem of finding the properties of the particle in some future time is nothing but to find the solution to the above set of differetial equations. This is the very case with all the problems in Physics. Therefore, we only need the tools to solve a general set of differential equations numerically using a computer. I can now start by describing the steps in order. Rather, I will start by describing an example and show you the path that I took to solve it; Molecular Dynamics (MD) of a gas with Lennard Jones potential.
Molecular Dynamics
I chose this example as it has enough complexity to show many of facets involved in numerical computation and also that many of you will be familiar with this problem.
Differential Equations of the System
We are considering a cloud of gas atoms in the NVT ensemble. Which is a fixed number of atoms in a fixed volume at a constant temperature. Why this particular picture? Given any gas in a volume, we know that the properties of the gas are independent of the volume, unless the volume is not small enough. Thus, we choose a volume with about a 100 atoms, which makes it easier for the program we write to simulate. These atoms jiggle around under the Newton’s equations of moiton and forces generated by the Lennard Jones potential. For the current scenario, as shown in the image1, we assume that the walls are rigid and the atoms collide with the wall elastically. The equations for such a system are the follwing:
$$ \begin{aligned} \frac{d\mathbf{x}}{dt} &= \mathbf{v}\newline \frac{d\mathbf{v}}{dt} &= \mathbf{F}/m \end{aligned} $$
Here, $\mathbf{x}$ and $\mathbf{v}$ are the 3D vectors denoting the position and velocity of a single atom. $\mathbf{F}$ is the total force on the atom from all other particles in the system. When two atoms are seperated by the vector $\mathbf{r}$, the force between them is given by
$$ \mathbf{F} = 48\frac{\epsilon}{\sigma}\big[ \Big( \frac{\sigma}{r}\Big)^{13} - 0.5\Big( \frac{\sigma}{r}\Big)^{7} \big]\hat{\mathbf{r}}$$
We will follow the following method to solve for the next state of our system after one time step:
- Calculate the forces on each of the particle from their position coordinates.
- calculate the acceleration of the particles and thus calculate the final velocity in the current time steps.
- Using the acceleration or the two velocities, i.e. the velocities at the end of the previous step and the velocities at the end of the current step, calculate the new positions of the particles.
This method as described, actually seems simple to understand but is very heavy computationally. For example, taking 10 atoms, at every time step we need to calculate the forces on one atom from every other atom. Roughly, that makes it a 100 calculations per time step. Further, the positons and the velocities of the particles need to be updated. We take some assumptions to simplify the calculations in some places.
Non-dimensionalise the equations to be used: We can see that the units of force as stated above is $MLT^{-2}$. To take these equations on to the numerical side is cumbersome as the constants involved are either too large or in this case too small. Further, it also makes it very difficult to debug the code if the equations are in the dimensional form. So we use these instead: $$ \tilde{\textbf{x}}=\frac{\textbf{x}}{\sigma}$$ $$ \tilde{\textbf{F}}=48\big[ \Big( \frac{1}{\tilde{r}}\Big)^{13} - 0.5\Big( \frac{1}{\tilde{r}}\Big)^{7} \big]\hat{\mathbf{r}}$$
Since the forces are only significant from the atoms which are near, we can ignore the ones that are far away using a cut-off radius. This makes sure that the computation in each step is not very heavy. We can use a cut-off radius looking at the LJ potential and a cut-off of $10 \ \sigma$ is good enough in this problem.
Given that we now have the tools required to simulate the system, let us get to the code for this approach.
Simulating the System
Using the above theory we can indeed simulate it in any language of our choice. I choose Julia for the reasons listed in this link. It is a very powerful language for the job and the package DifferentialEquations.jl or OrdinaryDiffEq.jl are more than capable for our application with advanced features for a more complicated setup.
We will first start by defining some constants:
#### This is a code trying to generate the molecular dynamics of gas molecules in a trapped volume #####
kb = BoltzmannConstant.val
## parameters for the LJ potential
ϵ = 1.65e-21 # in Joules
σ = 3.4e-10 # in meters
m = 6.69e-26 # mass of the atom in KG
#### constants for dimensionless parameters
τ = sqrt(m*σ^2/ϵ) ## time
r0 = σ
v0 = r0/τ
N = 2 # number of atoms
f0 = ϵ/σ # force
P0 = ϵ/σ^3 # pressure
T0 = ϵ/kb
l = 5 # length of the box in uinits of σ
r_cut = 10 # cut_off radius in units of σ
While writing your code, it is a good idea to make as many comments as possible to make it more clear for us or anyone else who might go through your code. Once, the required constants are defined, we go ahead for the most important part. The functions:
# defining the functions necessary for the system; required are force, potential energy, kinetic energy
function E_pot(pos,n1,n2) # defining the potential energy between two atoms
r = sqrt(sum(@. abs(pos[n1,:] - pos[n2,:])^2))
if n1==n2 # cutoff radius
return 0
end
return 4*((1/r)^12 - (1/r)^6)
end
function Potential_Energy(pos)
pot = 0
for n1=1:N
for n2=1:N
if n2>n1
pot += E_pot(pos,n1,n2)
end
end
end
return pot
end
function Kinetic_Energy(vel) # kinetic energy of the entire system
return sum(vel.^2)*0.5
end
Temperature(vel) = (2*Kinetic_Energy(vel)/(3*N-3))*(T0)
function force(pos,n1,n2)
vec = pos[n1,:] .- pos[n2,:]
if n1==n2 # implementing cutoff radius and avoiding force calculation from the same atom
return vec.*0
end
r = sqrt(sum(@. abs(vec)^2))
if r > r_cut
return vec.*0
end
return (48/r^2)*((1/r)^12 - 0.5*(1/r)^6).*vec
end
function force_T(pos)
force_mat = pos.*0
for n1=1:N
f = pos[1,:].*0
for n2=1:N
f = f.+ force(pos,n1,n2)
end
force_mat[n1,:] = f
end
return force_mat
end
The above functions are written poorly as it can be seen from the nested for loops and the unnecessary memory allocations which slow down the code drastically. We will take a look at methods to make them efficient in a different post.
Now, we are ready to test it out. Right now, we can go ahead and start using the solver from the OrdinaryDiffEq.jl. But, it would be very hard to go through the errors of the package and debug the code you have just written. Therefore, we will start with a manual integrating algorithm. Even though it is very inefficient, it would be a very good testing ground for our functions. We chose Velocity-Verlet algorithm here. Why? First, it is just a 2 step algorithm giving us a 2nd order accuracy and it is very easy to implement which makes it easy to test our code in the preliminary stage. The Velocity-Verlet algorithm has 4 calculations roughly in each step, with two force calculations as it seems. To reduce one of the force calculations, we can use memory to store the force calcualted in the previous step. $$ \begin{aligned} v(t+\Delta t/2) = v(t) + a(t)\Delta t/2\newline r(t+\Delta t) = r(t) + v(t + \Delta t/2) \Delta t\newline a(t + \Delta t) = F(r(t + \Delta t))/m\newline v(t + \Delta t) = v(t + \Delta t/2) + a(t + \Delta t )\Delta t/2 \end{aligned} $$
Do note that the above equations are not dimensionless. Once we setup our non-dimensional equations for the Velocity-Verlet algorithm, our force $\textbf{F}$ is nothing but the acceleration $a$ in the above equations, and the mass $m$ does not show up as it is absorbed into other nondimensional factors.
Before that, we need a way to initiate our problem and understand the time span at which the simulation should take place. Since we are just testing our code, we can start with two atoms with no other coordinate other than along the z-axis with opposite velocities. This makes sure that we have a collision to monitor. Further, in the process of non-dimensionalising the units of length and time are given as follows.
### initialising the system
## the following are used to test two particles head on;
x = x.*0
y = [0,0]#y.*0
z = [-0.75,0.75].*l
vx = [0.0,0.0]
vy = [0.0,0.0]
vz = [0.5,-0.5]
## done with test conditions
pos = hcat(x,y,z)
vel = hcat(vx,vy,vz)
#### constants for dimensionless parameters
τ = sqrt(m*σ^2/ϵ) ## time
r0 = σ
v0 = r0/τ
Thus, the time step $dt$ which is used will be in terms of $\tau$. Finally the reflective coundary conditions are implemented. All the code takes the below form when put together.
#### This block implements the Velocity-Verlet algorithm #### This is a code trying to generate the molecular dynamics of gas molecules in a trapped volume #####
N = 2 # number of atoms
dt = 1e-3 #in units of τ
#### This block implements the Velocity-Verlet algorithm using a manually written for-loop
@time begin
N = 2
pos,vel = initiate()
f_i = force_T(pos)
pos_list = []
KE=[]
PE=[]
for i=1:200000
global vel, pos, f_i
v_h = vel + 0.5*dt*f_i
pos = pos + v_h*dt
f = force_T(pos)
vel = v_h + 0.5*dt*f
f_i = f
# boundary conditions
while sum([abs(x) > l for x in pos]) > 0
atoms_crossed=findall(x->abs(x)>l,pos)
atoms_crossed=map(x->[x.I...],atoms_crossed)
for i in atoms_crossed
atom = pos[i[1],i[2]]
# pos[i[1],i[2]] = atom - 2*l*sign(atom) # periodic boundary condition
pos[i[1],i[2]] = sign(atom)*l + sign(-atom)*(abs(atom)-l)# reflective boundary condition
vel[i[1],i[2]] = -vel[i[1],i[2]]*1.00
end
end
if sum([abs(x) > 2*l for x in pos]) > 0
break
end
# done boundary conditions
# collecting parameters
if i%10==0 # collecting positions every 10 steps
append!(pos_list,pos)
end
append!(KE,Kinetic_Energy(vel))
append!(PE,+Potential_Energy(pos))
end
# end # end to time measurement
figure()
plot(KE+PE)
end
function atom_traj(n,pos_list)
(leng,) = size(pos_list)
data_pts = convert(Int64,leng/(N*3))
pos_n=zeros(data_pts,3)
for i=1:data_pts
pos_n[i,1] = pos_list[3*N*(i-1)+n]
pos_n[i,2] = pos_list[3*N*(i-1)+n+N]
pos_n[i,3] = pos_list[3*N*(i-1)+n+2*N]
end
return pos_n
end
figure()
for i=1:N # chose the atoms whose trajectory you want to plot
plot(atom_traj(i,pos_list)[:,3])
end
#### Manually written for loop done ###
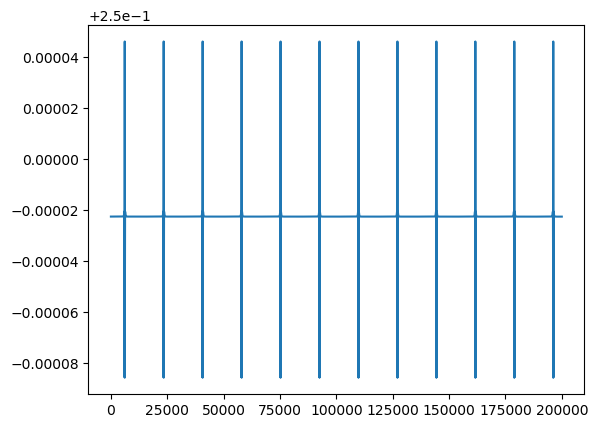
We can see in the last step of the code, that we choose the number of atoms whose trajectory we want to plot by using a function which fetches the position coordinates from the solution. This is just to make sure that the functions we defined are working as expected. The clues that we are looking for are whether the atoms are following the boundary conditions and whether the atoms collide because of the potential. By running the above code, we should get the solutions as below. Total Energy
z-coordinate of the two atoms
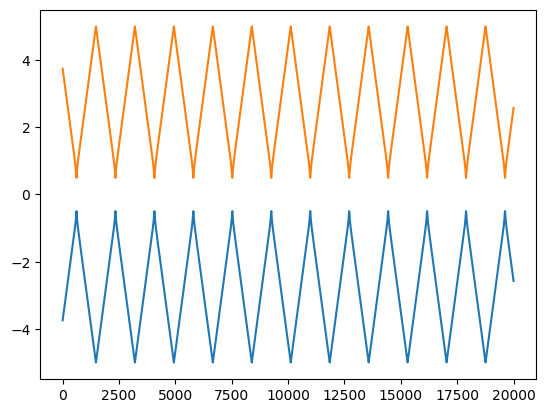
The energy curve shows that energy is not constant throuout the process. This should not be correct as there is no energy in-or-out through out the system. But, this is very normal in numerical calculations. In a collision, when the atoms are too close, the potential is very steep and cannot be monitored effectively given our time step. Thus, no matter how small the time step is, the spike in the energy cannot be eliminated completely, but can be reduced significantly by making the time step as small as possible. In our case, we can see that the spike in the total energy is of the order of $10^{-5}$ which is small enough for us. From the position plot of the two atoms, we find that the atoms repel each other and are pushed back, which is as expected. This is a very good sign, and it took some considerable time to get these results. If you fail getting them in the first few attempts, don’t feel too let down. It is alright and you will get here. We can now aim for something more complicated, a general case. Our functions, as written above, are ready to handle a general $N$ number of atoms. We will need a new function to initiate the positions and velocities of any N number of atoms. I use the following function for this reason.
# function to make a grid
flat_gridpoints(grids) = vec(collect(Iterators.product(grids...)))
# defining the positions of the atoms, in units of sigma
function initiate()
a = range(-0.99*l,stop=0.99*l,length=convert(Int64,ceil(sqrt(N)))+1)
req = flat_gridpoints((a,a,a))
req=[[x for x in i] for i in req]
final=req[1]
for i in req[2:end]
final=hcat(final,i)
end
grid = (transpose(final))
x = shuffle(grid[:,1])[1:N]
y = shuffle(grid[:,2])[1:N]
z = shuffle(grid[:,3])[1:N]
# defining the velocities of the atoms, in units of σ/τ
vx = (2 .*randn(N).-1).*0.5
vy = (2 .*randn(N).-1).*0.5
vz = (2 .*randn(N).-1).*0.5
pos = hcat(x,y,z)
vel = hcat(vx,vy,vz)
vel = vel .- sum(vel)/(3*N)
return pos,vel
end
The above function is written with the idea that the N number of atoms need to be distributed in way as to have a certain minimum distance between them. Thus, we make a grid which can at least have N points in it, and then randomly choose N points where the atoms are placed. In the first line of the function, note that the grid is also limited to $-0.99l$ to $0.99l$ so as to not keep any atom just on the boundary. With this initiating function, we can use the same manual for-loop to simulate the conditions. But, it is limited to Velocity-Verlet algorithm and is inefficient. We look for other symlectic integrators (the integrators which can maintain a constant energy through out the computation) as part of the OrdinaryDiffEq.jl package. I will leave the specific documentation to the official manual here. But, the final code comes out to be similar to the code block below.
#### This block uses the solver and a higher order symplectic solver to integrate the equations ##
N=2
@time begin
pos,vel = initiate()
while isnan(Potential_Energy(pos))
global pos,vel
pos,vel = initiate()
end
# sys_init = vcat(pos,vel)
function Force(v,u,p,t)
dv = force_T(u)
return dv
end
N_t = 40000
t_span=(0.0,N_t*dt)
######### implementing the continuous boundary condition using ContinuousCallback
# using an integrator to connect with the solver
condition(u,t,integrator) = sum([abs(x) > l for x in integrator.u.x[2]]) > 0
function affect!(integrator)
pos=integrator.u.x[2]
vel=integrator.u.x[1]
atoms_crossed=findall(x->abs(x)>l,pos)
atoms_crossed=map(x->[x.I...],atoms_crossed)
for i in atoms_crossed
atom = pos[i[1],i[2]]
# pos[i[1],i[2]] = atom - 2*l*sign(atom) # periodic boundary condition
pos[i[1],i[2]] = sign(atom)*l + sign(-atom)*(abs(atom)-l) # reflective boundary condition
vel[i[1],i[2]] = -vel[i[1],i[2]]
end
integrator.u = ArrayPartition(vel,pos)
end
cb = DiscreteCallback(condition,affect!)
# solving the problem
problem = SecondOrderODEProblem{false}(Force,vel,pos,t_span,callback=cb)
sol = solve(problem,VelocityVerlet(),dt=dt);
print("Done")
end
The above block of code is a test to see how to use the solver and its feature of callback to implement the boundary conditions in the system. Further, we have to plot the results to make sure that they match our manual for-loop with the follwoing plot function.
# plotting the solution
t = sol.t
(leng,)=size(t)
E=[]
z1 = []
z2 = []
for i=1:leng
if i%10==0
append!(E,Kinetic_Energy(sol.u[i].x[1]) + Potential_Energy(sol.u[i].x[2]))
pos = sol.u[i].x[2]
append!(z1,pos[1,3])
append!(z2,pos[2,3])
end
end
plot(E)
figure()
plot(z1)
plot(z2)
show()
Now that, we have the same results across our model can be extended for a 100 atoms and run it. We can calculate properties like the pressure exerted on the walls, temperature of the sample or its diffusion constant. But, before that let’s make it a bit interesting. In this particular solution, it is hard to maintain the temperature of the sample to be constant because of the many slightly inelastic collisions taking place. Thus, we need a thermostat to make sure that the temperature can be moderated to our wish. Here, we will use the Nose-Hoover thermostat for the problem.
Imagine that there is one extra particle in the system, which is not accounted for any other paramter except temperature. Now the velocity or the energy of that particle is what we will vary in a way as to keep the temprature as near as possible to the set temperature. I would not go into the main equations, but you can find them here. Finally, we end up with the following equations.
$$ \begin{aligned} \frac{d \mathbf{v}}{dt} &= \mathbf{F} - \zeta \mathbf{v}\newline \frac{d \zeta}{dt} &= \frac{1}{\Omega}\Big(T - T_{set} \Big) \end{aligned} $$ Omega is the factor that can be set to tune the reaction of the thermostat and $T$ is the temperature of the system calculated using the function defined in the earlier section. Finally, this correction can be introduced into the force function used along with the solver.
Note: When the equation for the time variation of $\zeta$ is used, we see that the temperature changes sinusoidally around the $T_{set}$ without settling. Using the learning from PID controller, we introduce the term $-10^{-4}\zeta$ to make sure that the system reaches a stable temperature. All the above can them be implemented as shown in the below code block.
#### This block uses the solver and a higher order symplectic solver to integrate the equations ##
### setting the parameters ###
N=20
ξ = 0
# ξ_list=[]
α = 0.5e-4
T_set = 373 # in Kelvin
dt = 0.0005
t_step = dt*25
t_span = (0.0,400)
####
@time begin
pos,vel = initiate()
while isnan(Potential_Energy(pos))
global pos,vel
pos,vel = initiate()
end
# sys_init = vcat(pos,vel)
function F(v,u,p,t)
global ξ
T = Temperature(v)
ξ += -1e-3*ξ + α*(T - T_set*(3*N+1-3)/(3*N-3))*t_step*0.5
# append!(ξ_list,ξ)
dv = force_T(u) .- ξ.*v
return dv
end
######### implementing the continuous boundary condition using ContinuousCallback
# using an integrator to connect with the solver
condition(u,t,integrator) = sum([abs(x) > l for x in integrator.u.x[2]]) > 0
function affect!(integrator)
pos=integrator.u.x[2]
vel=integrator.u.x[1]
friction = integrator.u.x[2][end,:]
atoms_crossed=findall(x->abs(x)>l,pos)
atoms_crossed=map(x->[x.I...],atoms_crossed)
for i in atoms_crossed
atom = pos[i[1],i[2]]
# pos[i[1],i[2]] = atom - 2*l*sign(atom) # periodic boundary condition
pos[i[1],i[2]] = sign(atom)*l + sign(-atom)*(abs(atom)-l) # reflective boundary condition
vel[i[1],i[2]] = -vel[i[1],i[2]]
end
if sum([abs(x) > 2*l for x in pos]) > 0
println("Solution exploded!!")
terminate!(integrator)
end
integrator.u = ArrayPartition(vel,pos)
end
cb = DiscreteCallback(condition,affect!)
problem = SecondOrderODEProblem{false}(F,vel,pos,t_span,callback=cb)
sol = solve(problem,VelocityVerlet(),dt=t_step);
println("Done")
run(`notify-send "Simulation Done" --icon="/usr/share/icons/Yaru/32x32/emblems/emblem-default.png"`);
end
I have included the small line to run a bash command notify-send to show a small notification when it is done. This is particularly useful as it takes about half-an-hour to an hour for it to complete. The final step is to plot it
# # plotting the solution
t = sol.t
(leng,)=size(t)
E=[]
T = []
for i=1:leng
append!(E,Kinetic_Energy(sol.u[i].x[1])+Potential_Energy(sol.u[i].x[2]))
append!(T,Temperature(sol.u[i].x[1]))
end
plot(E,label="Total Energy")
plot(T,label="Temp")
legend()
show()
We end up with the plot:
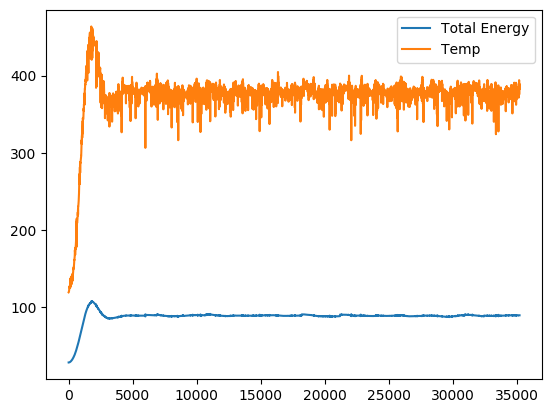
This plot clearly shows the thermostat in action. The temperature along with the total energy of the system settle nicely. In the above run, the set temperature was $373\ K$. This ends the simulation with the following points to improve on.
- It only works for a reflective boundary condition. For a periodic boundary, sometimes the atoms overlap with each other making a singularity in the calculation. Some extra code should be included to deal with that scenario.
- Calculate extra parameters like Pressure or diffusion constant of the gas.
I included the complete code in my Github page.
Summary - Be Careful rather than to waste time Debugging!
From my experience, I think the following steps need to be followed to make a numerical simulation.
- Never ever start to write code before you are ready with a set of non-dimensionalised equations for your system; tried it, it only makes it very cumbersome.
- Make sure that you verify the functions that you defined before going to the next step of using them. For example, in the above simulation we need to check if the force functions are working correctly in a special case for only two atoms. Only then, should we go ahead to use them on a general case. I made the same mistake and wasted many valuable hours on simple bugs.
- Make plots wherever possible and compare it with the data you already have; Here, make a plot of force between atoms with respect to the distance between them. This is a very good way to check and understand the properties of the system.
I hope that this post is helpful to many of you who are just about to get started with some numerical simulations in physics. Feel free to comment or ask any question that you might have in this regard.
comments powered by Disqus